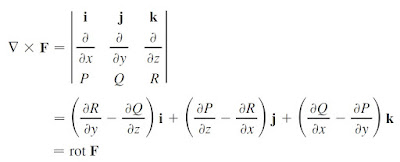EXAMEN FINAL CONJUNTO

El examen se llevo a cabo en el aula 501 del ICB en el horario de 17:00-19:00

Clase Nº 33

En esta ocasión, se tuvo una clase extra, con el objetivo de realizar ejercicios de preparación para el examen del mismo día, los ejercicios constaron de los temas principales de la materia recibida el segundo bimestre.

A continuación se adjuntan algunos ejemplos

Clase Nº 32

Teorema de Green
El teorema de Green proporciona la correspondencia entre una integral de línea alrededor de una curva simple cerrada C y una integral doble sobre la región plana D limitada por C.

Suponga que la D consta de todos los puntos del interior de C, así como de todos los puntos sobre C.) En el planteamiento del teorema de Green se usa la convención de que la orientación positiva de una curva simple cerrada C se refiere a un recorrido sencillo de C en el sentido contrario al de las manecillas del reloj.

A continuación se adjuntan algunos ejemplos:

Bibliografía:

J. Stewart, Cálculo en Varias Variables, Cengage Learning.

Clase Nº 31

Primero se llevó acabo la corrección de la última evaluación.

Teorema Fundamental de las integrales de línea

Se puede expresar como:

Independencia de la Trayectoria

A continuación se adjuntan algunos ejemplos:

Bibliografía:

J. Stewart, Cálculo en Varias Variables, Cengage Learning.

SEGUNDA PRUEBA DEL SEGUNDO BIMESTRE

Clase Nº 30

Integral de línea de primera especie

Integral de linea de segunda especie

A continuación se puede observar de mejor manera estos temas:

Bibliografía:

http://matematica1.com/integral-de-linea-y-de-superficie-ejercicios-y-problemas-resueltos-pdf/

Clase Nº 29

Condiciones para que una integral de línea sea uniforme

1. f(x,y) , fx , fy son continuas.
2. C es una curva uniforme y r`(t) es diferente de cero.

A continuación se adjuntan algunos ejercicios adicionales.

Clase Nº 28

Rotacional de un campo vectorial conservativo

Laplaciano de un campo Escalar

Se denomina Laplaciano:

Función Armónica

Se denomina como función armónica al laplaciano igual a 0.

Integrales de Línea

En este caso la definición de integral de línea es la misma que la integral en un intervalo [a,b], con la diferencia que en este caso se integra sobre la curva C.

Estas integrales se denominan también integrales curvilíneas.

Se utilizan para el cálculo de flujo  de fluidos, fuerzas, electricidad y magnetismo.

Definición:

 Si f se define en una curva C uniforme definida por:

Entonces la integral de línea de f a lo largo de la curva C es:

Si el límite existe.

La longitud de la curva C es:

Si f es continua y C es una curva uniforme, entonces el límite existe y se cumple:

Bibliografía:

J. Stewart, Cálculo en Varias Variables, Cengage Learning.