Clase Nº 3

El Plano

En comparación con una recta; Un solo vector paralelo al plano es insuficiente para llevar la “dirección” del plano, pero un vector perpendicular al plano especifica por completo su dirección.

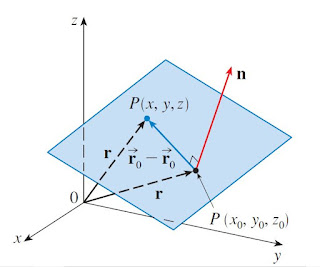
Así, un plano en el espacio se determina por un punto P(x,y,z) en el plano y un vector 'n' que es ortogonal al plano. Este vector ortogonal n se llama vector normal.

El vector normal n es ortogonal a todo vector en el plano dado. En particular, n es ortogonal a r-ro y, por lo tanto, se tiene: 

$$n\cdot (r-{ r }_{ 0 })=0$$

A la ecuación anterior se la conoce como ecuación vectorial del plano.

Si a esta ecuación se le asignan los valores:

$$n=(a,b,c)\\ r=(x,y,z)\\ { r }_{ 0 }=({ x }_{ 0 },{ \quad y }_{ 0 },{ \quad z }_{ 0 })$$

Se obtiene:

$$\left< a,b,c \right> \cdot \left< x-{ x }_{ 0 },y-{ y }_{ 0 },z-{ z }_{ 0 } \right> =0\\ a(x-{ x }_{ 0 })+b(y-{ y }_{ 0 })+c(z-{ z }_{ 0 })=0$$

Esta es la ecuación general del plano, o ecuación escalar del plano.

$$Ax+By+Cz+D=0$$

Ecuación segmentaria del plano

Si se conoce los puntos de corte del plano con los ejes coordenados, se puede escribir los otra ecuación del plano llamada segmentaria.

Partiendo de la ecuación general del plano, se puede obtener la ecuación segmentaria del plano.

$$Ax+By+Cz+D=0$$

$$Ax+By+Cz=-D$$

$$\frac { Ax }{ -D } +\frac { By }{ -D } +\frac { Cz }{ -D } =1$$

$$\frac { x }{ -\frac { D }{ A }  } +\frac { y }{ -\frac { D }{ B }  } +\frac { z }{ -\frac { D }{ C }  } =1$$

Obteniendo:

$$\frac { x }{ a } +\frac { y }{ b } +\frac { z }{ c } =1$$

En donde:

$$a=-\frac { D }{ A } ;\quad b=-\frac { D }{ B } ;\quad c=-\frac { D }{ C } $$

Es decir segmentos en el eje ox, oy, oz respectivamente.

Ecuación Normal del Plano

En el siguiente enlace se puede observar una demostración de las diferentes ecuaciones del plano que han sido vistas en esta clase.

Bibliografía:

J, Stewart, Cálculo en Varias Variables, Cengage Learning

Tomado de: http://slideplayer.es/slide/34612/